I write about evolutionary anthropology, behavioral sciences, and related AI, particularly small, specialized Deep Neural Networks and LLMs.
Functions - Discrete Mathematics
2.101 Introduction to functions
See references 1, 2
Definition:
A function is a relation between a set of inputs A and a set of outputs B.
Each input maps to exactly one output.
Multiple items in A can map to a single item in B.
Example of a function:
- each item A has an output in B
- 65 has no output
- 62 has 2 outputs
We write:
We write:
y is called the image of x,
whereas x is called the pre-image of y.
We write:
$$ f(x) = y $$
Example:
A = {0, 1, 2, 3, 4, ...}
B = {0, 1, 2, 3, 4, ...}
$ x \rightarrow 2x+1 $- any number squared is positive
- +1 makes for bigger than 1
Plotting Functions
Linear Functions
- straight line function
- passes through the point (0, b)
- a is the gradient
- if gradient a > 0 then the function is increasing
- $ x_1 < x_2 $ then $ f(x_1) < f(x_2) $
Quadratic Functions
$$ f(x) = ax^2 + bx = c $$
- where a, b, and c are the numbers and a $ \neq $ 0
Exponential Function
$$ f(x) = b^x \ where \ b > 0 \ and \ b \neq 1 $$
- variable b is called the base of the function
- Domain $ ]-\infty, \infty[ $
- Range $ ]0, \infty[ $
- Horizontal asymptote y= 0
Laws of Exponents
$ b^x \cdot b^y = b^{x+y} $
$ \frac{b^x}{b^y} = b^{x-y} $
$ (b^x)^y = b^{xy} $
$ (ab)^x = a^x \cdot b^x $
$ (\frac{a}{b})^x = \frac{a^x}{b^x} $Natural Logarithm function
see reference 4
2.106 Injective and surjective functions
see reference 5
Injective (one-to-one) Functions
- one-to-one function
- Let $ f: A \rightarrow B $ be a function
- Definition: f is said to be an injective (one-to-one) function if and only if:
- for all $ a,b \in A $, if $ a \neq b $ then $ f(a) \neq f(b) $
Surjective (onto) functions
Resources
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/dEASs/2-101-introduction
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/dEASs/2-101-introduction
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/LJ9wV/2-104-plotting-functions
- https://www.youtube.com/watch?v=8qs6QxGCIQU
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/XyWA9/2-106-injective-and-surjective-functions
Munkres Assignment - Hungarian Algorithm
Hungarian Algorithm
The following videos show how, but not why:
Resources
- https://en.wikipedia.org/wiki/Hungarian_algorithm
- https://www.youtube.com/watch?v=cQ5MsiGaDY8
- https://www.youtube.com/watch?v=FCaD34z--bY
- https://www.youtube.com/watch?v=eXiUYlEb__k
- https://www.youtube.com/watch?v=cVBzMXYc4ss
master of many trades
Jack of all trades, a master of none,I prefer better than a master of one.
Non-integer numbers conversion - Computational Mathematics CM1015
Non-integer numbers conversion
How do you convert decimal fractions to binary?
How to convert a binary fractional number to a base 10 number?
see reference 2
Convert the decimal number 11.625 into binary
$ 11 \color{red} {.625}_{10} $
What is the decimal number 0.03125 in binary?
2 * 0.03125 = 0.0625 = 0 + 0.0625
2 * 0.06250 = 0.1250 = 0 + 0.1250
2 * 0.12500 = 0.2500 = 0 + 0.2500
Operations with binary numbers
See reference 3Addition of binary numbers
$ 1110 $ \\ carry-over numbers
$ 0101_2 + $
$ 0111_2 = $
$ \overline{1100}_2 $
Subtraction of binary numbers
$ 110 - $ \\ 6 decimal
$ \overline{0 0 1}_2 $ \\ 1 decimal
Multiplication of binary numbers
Division of binary numbers
Number bases webinar video
"The only time you are getting better is when you are stuck.- So, embrace being stuck! "
Extra video: numbers 1
- prime numbers
- highest known prime number $ 2^{77232917} - 1$
- exponentials
- $ x^0 = 1 $
- $ x^1 = x $
- $ x^2 = x * x $
- $ x^{-1} = \frac{1}{x} $
- $ x^{-2} = \frac{1}{x*x} = \frac{1}{x^2} $
- $ x^{-n} = \frac{1}{x^n} $
Extra video: numbers 2
- see reference 6
- base ten fractional
- what is the lowest base you can have
- base 2
- conversion exercises
References
- https://www.coursera.org/learn/uol-cm1015-computational-mathematics/lecture/wrj47/non-integer-numbers-conversion
- https://www.coursera.org/learn/uol-cm1015-computational-mathematics/quiz/QW8GL/topic-1-lesson-3
- https://www.coursera.org/learn/uol-cm1015-computational-mathematics/lecture/0qco4/operations-with-binary-numbers
- https://www.coursera.org/learn/uol-cm1015-computational-mathematics/lecture/y71es/number-bases-webinar-video
- https://www.coursera.org/learn/uol-cm1015-computational-mathematics/lecture/K02pr/extra-video-numbers-1
- https://www.coursera.org/learn/uol-cm1015-computational-mathematics/lecture/lHwNt/extra-video-numbers-2
- https://docs.google.com/spreadsheets/d/19zWX5qNcfVwG37VUSi0aeCMfNSOwhq1MMNtdwguyk5k/edit#gid=0
- https://calculator.name/baseconvert/quinary/decimal/1212
Non-integer numbers conversion - Computational mathematics - UoL
Non-integer numbers conversion
= 10 + 7 + \frac{3}{10} + \frac{7}{100} + \frac{5}{1000} $
Choosing between MacOS iMovie (free) and Final Cut Pro ($299)
Choosing between MacOS iMovie (free) and Final Cut Pro ($299)
Set Theory - Discrete Mathematics
Set Theory - Introduction to discrete mathematics
the fundamental concept of sets, functions, logic, graphs, trees, relations,
combinatorics, mathematical induction, and recursive relations.
Syllabus
Webinar
What is the definition of Sets?
collection of objects.
Mathematicians use, the term is set to refer to a well-defined, unordered, collection of any kind of object, duplicates are allowed.
The empty set is a set that contains nothing.
- an element of a set
- belongs in $ \in $
- not belong in $ \notin $
- the cardinality of a set
- Definition: Given a set S, the cardinality of S is the number of elements contained in S. We write the cardinality of S as |S|.
- Given V = {a,e,i,o,u}; |V| = 5
- |E| = |{}| = $ | \emptyset | $ = $ | \varnothing | $ = 0
Subset
- A is a subset of B if every element of A also belongs to B.
- A is also an element of B. $ A \subseteq B $
- subset \subset
- not subset equal $ \not \subseteq$
- subset not equal $ \subsetneqq $
- subset not equal $ \subsetneq $
- if V = {a,e,i,o,u} AND W={u,w}$ \implies W \subsetneq V $
- Special sets
- N all natural numbers N = {1,2,3,..., \infty}
- Z all integers $ \mathbb{Z} $ = {..., -3,-2,-1,0, 1,2,...}
- The notation $ \mathbb{Z} $ for the set of integers comes from the German word Zahlen, which means "numbers".
- positive integers < 4 = {2}
- Q all rational numbers such as a/b where $ b \neq 0$
- $ Q = \{ \frac{n}{m} | n,m \in \mathbb{R} \ and \ m \ne 0 \} $
- R or $ \mathbb{R} $ all real numbers
The listing method and rule of inclusion
- Set representation
- Listing method
- list all elements of the set
- V = {a,e,i,o,u}
- Set builder notation
- example $ Even = \{ 2n | n \in \mathbb{R} \} $
- example $ Odd = \{ 2n+1 | n \in \mathbb{R} \} $
- Q all rational numbers = $ Q = \{ \frac{n}{m} | n,m \in \mathbb{R} \ and \ m \ne 0 \} $
$ S_4 = \{ \frac{1}{2}, \frac{1}{4}, \frac{1}{6}, \frac{1}{8}, \frac{1}{10} \} \implies $
The powerset of a set
{1, 2, 3, 4}
{5, 6,}
$ X \subseteq A, \ but \ X \in B $
- The power set of the set
- definition:
- Given a set S, the powerset of S, written P(S),
is the set containing ALL the subsets of S. - Given S = {1, 2, 3}
- all subsets:
- {}
- {1}, {2},{3}
- {1,2},{1,3},{2,3}
- {1,2,3}
- then P(S)={{},{1}, {2},{3},{1,2},{1,3},{2,3},{1,2,3}}
Cardinality
- then P(S) = $ 2^{|S|} $
- P(S)={{},{1}, {2},{3},{1,2},{1,3},{2,3},{1,2,3}}
- |P(S)| = 2^{|S|} = $ 2^3 = 8 $
- $ |P(A)| = 2^{|A|} = 2^n $
- $ |P(P(A))| = 2^{|P(A)|} = 2^{2^n} $
- $ |P(P(P(A)))| = 2^{|P(P(A))|} = 2^{2^{2^{n}}} $
Powers of 2
$ 2^2 = 4 $
$ 2^3 = 8 $
$ 2^4 = 16 $
$ 2^5 = 32 $
$ 2^6 = 64 $
$ 2^7 = 128 $
$ 2^8 = 256 $
$ 2^9 = 512 $
$ 2^{10} = 1,024 $
$ 2^{12} = 4,096 $
$ 2^{13} = 8,192 $
$ 2^{14} = 16,384 $
$ 2^{15} = 32,768 $
$ 2^{16} = 65,536 $
$ 2^{17} = 131,072 $
$ 2^{18} = 262,144 $
$ 2^{19} = 524,288 $
$ 2^{20} = 1,048,576 $
Set Operations
Disjointed Sets (nothing in common)
Definition:
Two sets are disjointed if the intersection is zero.
$$ A \cap B = \varnothing $$
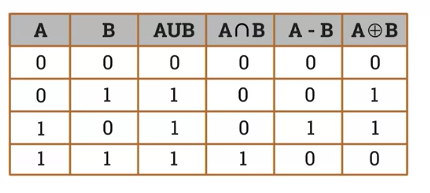
Set Union (all together)
Given two sets A and B,
the union of A and B, written $ A \cup B $,
contains all the elements in either A or B.
Set Intersection (common)
Given two sets A and B,
the intersection of A and B, written $ A \cap B $,
contains all the elements in both A and B.
Set Difference (one but not the other)
Definition:Given two sets A and B,
the set difference, written $ A - B $,
contains all the elements that are in A, but not in B.
Symmetric difference (owned separately)
Given two sets A and B,
the symmetric difference, written $ A \oplus B $,
- A \oplus B == "$ A \oplus B $"
- A \triangle B == "$ A \triangle B $"
- A \Theta B == "$ A \Theta B $"
- A \triangledown B == "$ A \triangledown B $"
Membership Table
Disjoint Sets
Equivalently, two disjoint sets are sets whose intersection is the empty set.
For example,
The representation of a set using Venn diagrams
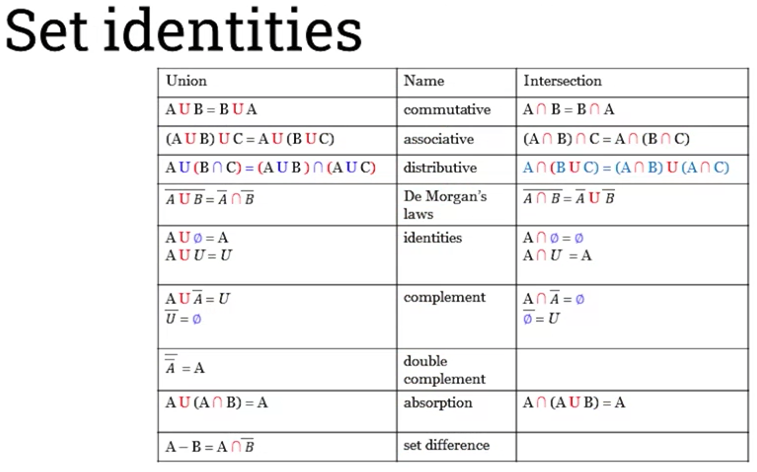
Augustus De Morgan's laws
$ A \cap \overline{ \overline{A} \cup \overline{B}} = A \cap \{2\} = \{1, 2\} \cap \{2\} = \{2\} $
$ \{2\} = A \cap B $
Exercise:
Given two sets A and B,
$$ \overline{ \overline{ A} \cup \overline{ B} } = A \cap B $$
$ A - \overline{B} = \{1, 2 \} - \{ 1, 4 \} = {4} = \overline{ A \cup B}$
Laws of sets: Commutative, associative, and distributives
Commutative
order does not affect the outcome.
- addition 2+3 = 3+2
- multiplication 2*3 = 3*2
- union $ A \cup B = B \cup A $
- intersection $ A \cap B = B \cap A $
- symmetric difference $ A \oplus B = B \oplus A $
- Subtraction $ 3-1 \neq 1-3 $
- Set difference $ A-B \neq B-A $
Associativity
concerns the grouping of elements in an operation.
- addition (a+b)+c = a +(b+c)
- multiplication (a*b)*c = a *(b*c)
- union $ (A \cup B) \cup C = A \cup (B \cup C) $
- intersection $ (A \cap B) \cap C = A \cap (B \cap C) $
- symmetric difference $ (A \oplus B) \oplus C = A \oplus (B \oplus C) $
- set difference $ (A - B) - C \neq A - (B - C) $
Distributivity
Using set identities to simplify expressions
Prove
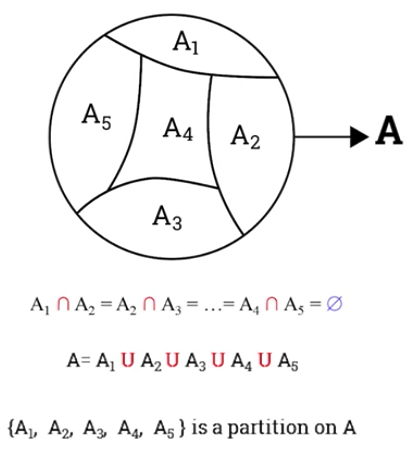
Partition of a set
all the subsets $ A_i $ are disjointed,
Exercise
$ | A \cup B | = | A | + | B | - | A \cap B | $
The formula expresses the fact that the sum of the sizes of the two sets may be too large since some elements may be counted twice. The double-counted elements are those in the intersection of the two sets and the count is corrected by subtracting the size of the intersection.
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
Given three sets A, B, and C, prove that:
$ | C \cup (A \cup B) | = | A\cup B \cup C | = $
Use the listing method to list the elements of the following sets:
$ A \cap \overline{B} = \{0, 2, 4, ..., 16, 18 \} \cap \{ 0, 2, 4, ..., 16, 18 \} = A = \{ 0, 2, 4, ..., 16, 18 \} $
Peer reviews
Read Book
Discrete Mathematics with Applications
Thomas Koshy
pp.70-71, 71-73, and 78-86.
Please also complete the following exercises:
pp.93, exercises 5–14, 27-32, and 57-60.
Review Problem Sheet
TODO: review and documentSummative Quiz
Webinar
References
- https://en.wikipedia.org/wiki/Set_(mathematics)
- https://en.wikipedia.org/wiki/Real_number
- https://en.wikipedia.org/wiki/Cardinality
- https://proofwiki.org/wiki/Symbols:Set_Theory/Symmetric_Difference
- https://en.wikipedia.org/wiki/Disjoint_sets
- https://en.wikipedia.org/wiki/Venn_diagram
- https://en.wikipedia.org/wiki/De_Morgan%27s_laws
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/QEPbf/1-205-laws-of-sets-commutative-associative-and-distributives
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/FuScz/1-207-partition-of-a-set
- Discrete Mathematics with Applications - Thomas Koshy
Post Scriptum
I am preparing to cancel the subscription to the e-mail newsletter that sends my articles.
Follow me on:
X.com (Twitter)
Google Scholar
My favorite quotations..
“A man should be able to change a diaper, plan an invasion, butcher a hog, conn a ship, design a building, write a sonnet, balance accounts, build a wall, set a bone, comfort the dying, take orders, give orders, cooperate, act alone, solve equations, analyze a new problem, pitch manure, program a computer, cook a tasty meal, fight efficiently, die gallantly. Specialization is for insects.” by Robert A. Heinlein
"We are but habits and memories we chose to carry along." ~ Uki D. Lucas
Popular Recent Posts
-
In my journey building software and managing technology teams, I've often witnessed the allure and danger of what Melissa Perri aptly na...
-
This is an example of an entertaining, AI-generated fictional story posing as “real-life stories”. I believe this “posing” should be outlawe...
-
I tested to belong to Haplogroup R1b1b2a1a1d1. Subclade R1b1b2a1a1d1* (as named by 23andMe ) or R1b1a2a1a1a4 (per FTDNA ) is a paternal (...
-
Physics and the laws of relativity: in parent-child relationship sound waves reach the subject after 25 years.
-
I am pleased with the performance and depth of the 32B Qwen MLX, running locally on my Mac Studio M1 with 64GB of RAM. 9 tokens per second ...
-
I decided to write down a few thoughts to clarify my obsessions with creating the "multitude" of AI agents that rely on the privat...
-
In my LM Studio, I have been using the 12 billion and 24 billion parameter models on my relatively inexpensive Mac Studio M1, which has 64 G...
-
I have run a quick test on a few LLM models I have installed locally on Mac OS with 64 GB of RAM. The test was conducted in English, but it ...
Most Popular Articles
-
In my journey building software and managing technology teams, I've often witnessed the allure and danger of what Melissa Perri aptly na...
-
Choice D Since we are currently renting, we started looking at the houses we could afford. This place fits our budget, but the baby blue col...
-
I have noticed a very unsettling statistic on my blog. This prompted a fascinating question about AI, blogs' future, and maybe even the...
-
I tested to belong to Haplogroup R1b1b2a1a1d1. Subclade R1b1b2a1a1d1* (as named by 23andMe ) or R1b1a2a1a1a4 (per FTDNA ) is a paternal (...
-
This is an example of an entertaining, AI-generated fictional story posing as “real-life stories”. I believe this “posing” should be outlawe...
-
I decided to write down a few thoughts to clarify my obsessions with creating the "multitude" of AI agents that rely on the privat...
-
I have run a quick test on a few LLM models I have installed locally on Mac OS with 64 GB of RAM. The test was conducted in English, but it ...
-
Prompt: What do you really see in the selfie of myself? AI: I see a volcano about to blow up and I see a lost, scared boy in front of it. ...